Vehicle Control
A parallel hybrid electric vehicle energy management strategy using stochastic model predictive control with road grade preview
Xiangrui Zeng et al. IEEE transaction on control system technology, 2015, link tags:#mdp,#sdp,#dp
progress: 60%
- Term:
- HEV: hybrid electric vehicles
- ECMS: equivalent consumption minimization strategy
- SoC: state-of-charge
主要工作:
- 用MDP和stochastic dynamic programming解决路况不确定(如有多条可行路径)下的HEV的能量管理问题(state-of-charge, SoC,何时充放电)。
- 现有方法缺陷:
- Dynamic programming:需要complete driving cycle information才可应用,但在实际中很难满足。
- Heuristic rules,fuzzy logic,ECMS不需要任何知识,但通常建立在standard driving cycle的基础上,对其它驾驶场景无法保证性能。
- MPC一般在standard driving cycle表现性能较好, 需要已知short-term路况信息(接下来的路程,车速,等)。实际中future route并非一直可用。long-term信息不确定(如红绿灯),影响预测效果。
上述问题的解决方案:将stochastic road grade信息和stochastic turn/stop信息与MPC联动
该解决方案存在的问题:需要一个较长时间的预测,但会受一些因素的影响
- 若step length不变,prediction horizon延长(增加预测点数量),长期的预测效果变差。
- 若通过延长step length的方法延长prediction horizon, 模型将变得不准确,因为模型本身有一个工作频率,此举使得预测频率与采样频率不同步。
- 本文工作:
- Developed a discrete model with large time-steps for HEVs,使得prediction horizon比传统MPC方法更长。
- 用finite-state MDP的框架对问题进行描述,并用stochastic dynamic programming (SDP)求解
需要一些假设:
- 未来的行径路线未知
- 当前位置、方向可知
- 附近路线的地形数据已知
- light traffic(简化问题,以及heavy traffic状态下对长期预测的意义不大)
存在的问题:
- 使用CPU运算,时间较长,需要10~100s。若设法将运算时间控制在10s之内,则可能可以应用于对较长road segments的实时预测。
方法:
- MPC中的求解预测序列的optimal control采用SDP
| Item | Detail |
|---|---|
| 系统模型System model | 两种情况,模型均给定,一段road segment只可能对应一种模型Case 1: steady-state models Case 2: |
| cost function | running cost: fuel consumption terminal cost:Consumed electricity energy |
| 限制条件 Constraints | 电池充上限及放电下限 |
| 优化器 Optimizer | SDP |
-
SDP solution backward induction algorithm(我认为可以理解为value iteration)
where is short for :optimal total remaining cost at the th step when the state vector is :第 步应选取的最优action
-
MDP的要素:
Item Detail State state vector包含:SoC value,road grade,speed limit,是否有stop/turn Action 车辆input Transition 历史交通数据中车辆选择某条路径的概率(类似于MC) Reward 与MPC共公用cost
Finites-state Markov chain for road grade
- 两个基本假设
- state变量只能在finite-state space
中取值。 - 之后的取值(future value)的概率分布只取决于当前的值(current value)因此独立于过去的取值。
- state变量只能在finite-state space
- 模型:
- road grade序列:
, 。其中 是road grade set, 是常数。 - 条件转移概率的定义为
是 的矩阵 中的元素
- road grade序列:
A two-level stochastic approach to optimize the energy managemetn strategy for fixed-route hybrid electric vehicles
Xiangrui Zeng et al., Mechatronics 2015, link
progress: 60%
主要工作:
- 采用异构的方式优化固定线路HEV的energy management strategy。
- High-level: SDP, 2D-table查找
- Low-level: control strategy,key parameters由high-level决定
- 假设:
- 车辆只在固定线路上运行,或经常在固定线路上运行, 并且可以通过某种方式识别出来。
- 历史驾驶数据已知。
方法
-
一些前提:
- 速度和能量之间没有直接关系(even if the speed profile looks similar, the energy demands could be quite diverse) 同一个条路径上每次测试数据相差很大
- Fixed-routebuneng cannot be considered as determined cycle. Not easy to construct an “average trip”
- Trip prediction is no very necessary for HEV energy management strategies unless the battery SOC may hit the boundaries of tis range. 除非会导致电池充放电的限度,否则没有必要对路径进行预测
-
Low-level只对当前道路分段(road segment)有效,不需要具有长期的知识或后续状态 Deterministic 可以采用ECMS,rule-based,fuzzy或MPC,可以实现实时运算 本文采用ECMS。
: a tuning parameter in the energy management strategy
-
High-level
-
即使对于给定的
, (电池SOC状态)和 (燃油消耗)为随机变量,但具有一定统计规律 -
每个state的approximated probability density distribution由统计历史数据得到
-
(分段是如何进行的?人工选取?)
-
过程:
- 从初始状态,电池部分充电,已知SOC,已知路段
- 选定某一个参数,交由low-level control
- 行驶至下一路段时,因路面随机情况,SOC将是一个符合一定统计分布的随机变量
- 直至行驶至终点
- 通过SDP,找出每个状态的value,从而确定应如何选定参数
-
用SDP的方法计算得到2D table 其形式为:分段开始时电池状态
(离散化) 分段序号 每个 对应一个 price factor(表征燃油价值与电能价值在此种情况下哪个更经济) -
查表结果:由进入某一路径分段时初始的SoC决定了建议配置燃油与电能的使用系数
-
DP的要素:
Item Detail State 电池初始SoC与路程分段的所有组合 Action 某种low-level control parameter(已离散化) Transition 在某个low-level control下到达下一分段时不同SOC的概率 Reward total cost =running cost + terminal cost 也是value iteration
-
A stochastic driver pedal behavior model incorporating road information
Xiangrui Zeng, et al., IEEE Transactions on Human-Machine Systems, 2017, link
Progress: 30%.
主要工作:
- 如何将driver’s pedal behavior分解为a sequence of actions并加以描述。
- 将车辆信息和路面信息作为输入,pedal action作为输出,使用input-output hidden Markov model (IOHMM)来描述pedal behavior。
- 设计了state transition,output distribution function。输入和输出的关键变量用统计的方法建模(generalized estimation-maximization method)与分析。
- 用模型可以区分驾驶风格,可以预测1-60s的行为。
方法:
-
IOHMM:
- Input
: can be large number - Hidden state
: can represent the unkown driver’s driving mode State transition可以以矩阵 和矩阵向量乘法表示 ( 是 的的probability distribution vector) - Output
的probability distribution为 - Model: can be nonlinear, parameters can ben identified offline. 当前所处的状态的概率分布由前一状态,当前输入决定。当前输出的概率分布由当前状态和当前输入决定。(听起来有点像Kalman filter)
- Input
-
发现:Intermittent pedal adjustments(断续踏板控制) 驾驶者不是在积极的随时调整对踏板的控制,而是调整—保持—调整。
结果
- Constant pedal model在长期预测中表现不好。
- ARX model are not suitable for pedal position prediction in these time scales. It cannot provide good prediction results even if its parameters are identified in real time.
- PID model只在长期预测中表现良好,因为此时道路环境限制为主要因素。
- IOHMM在长/短期预测中均表现良好
Real-time energy optimization of HEVs under connected environment: ECOSM 2021 benchmark problem and a case study
Fuguo Xu et al. , E-COSM 2021, link
progress: 40%
- Terms
- V2V: vehicle-to-vehicle
- V2I: vehicle-to-infrastructure
- V2X: (section 3.3)包含Ego vehicle sensor,geographical information(道路长度,路口位置,坡度)和traffic participants(V2V和V2I)
- ENG: engine
- MG1: generator
- MG2: motor
- SOC: state of charge
: engine torque : motor torque : generator torque
主要工作
- 问题:在有坡道的道路上的HEV的energy efficiency control。解决车辆的燃油经济性控制同时保证驾驶安全性和时效性。
- 假设:HEV有充足的外部实时信息,如geographic information,vehicle-to-infrastructure information和vehicle-to-vehicle information
- 提供了一个模拟器:industrial-level HEV model, traffic scenario database,running route based on real-world data
System
- controller
-
控制器输入: use any output signal of Plant Model and any signal of the V2X, section 3.1.3 line 130(V2X参见terms,包含地理信息,车辆信息和V2I及V2V)。
V2X包含的信息

Plant model可以提供的信息

Traffic scenario block (section 3.1.2)
项目 note Ego vehicle speed [m/s] Vehicle speed distance [m] Vehicle running distance acceleration [m/s^2] Vehicle acceleration Sensor of ego vehicle flag Sensor detection flag. 0 mean no detection; 1 means detection of preceding vehicle. WHen Platform_flag = 1, detection flag is 'nan', no signal from Simulink dist_headway [m] distance headway, when flag=0, it is 0
班距/与前车的距离(p19, line 220)V2V (vehicle-to-vehicle) pre_speed [m/s] Preceding vehicle speed
前车速度pre_distance [m] Preceding vehicle running distance
前车行驶的距离pre_acceleration [m/s^2] Preceding vehicle acceleration V2I (vehicle-to-infrastructure) state_next_1st [-] the phase of 1st next traffic light tRemain_next_1st [s] the remaining time of 1st next traffic light s2inters_next_1st [m] distance to the 1st next intersection state_next_2nd [-] the phase of 2nd next traffic light tRemain_next_2nd [s] the remaining time of 2nd next traffic light s2inters_next_2st [m] distance to the 2nd next intersection - 在section 3.1.2的traffic scenario中未提到geographical information??
-
控制器输出:
- TQ_eng_trg[Nm]:engine扭矩
- TQ_mg1_trg[Nm]:MG1(generator)扭矩
- TQ_mg2_trg[Nm]:MG2(motor)扭矩
- F_brake[N]:液压刹车力度
-
优化过程
- 约束
- Physical constraints
- 扭矩torque(engine, motor, generator)
- 速度N,rpm(engine, motor, generator)
- 电池输出功率PW_batt_out, Battery output power, kW
- 电池充电状态SOC,百分比
- Boundary constraints
- 和前车保持安全距离
- 红灯不越过停止线stop before the stop line
- Physical constraints
- 优化指标Index performance
- Speed limitation (不超速)
- Traffic collision (保持安全距离)
- Distance headway Run the light (到前方红绿灯的距离)
- Total travel time.
- 一些假设:
- 路线是直的(固定路线),没有拐弯
- 全程不超车(p19, line 231)
- 约束
-
- Plant model (given)
- 评判标准Scoring
- 判定失败:超速,追尾前车,闯红灯超过两次,长时间未保持安全距离(安全距离由绝对距离和车速度决定),用时过长
- 能源消耗(燃油消耗及SOC在出发和抵达时的变化),总用时(全程禁止超车,超车记为碰撞)
参考控制器模型
- block diagram
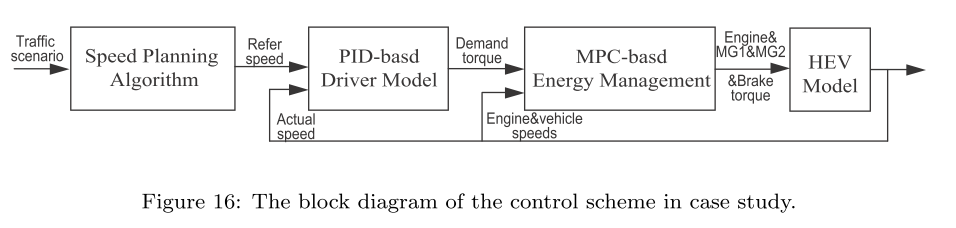
- Speed planning
-
一系列判断条件
框图
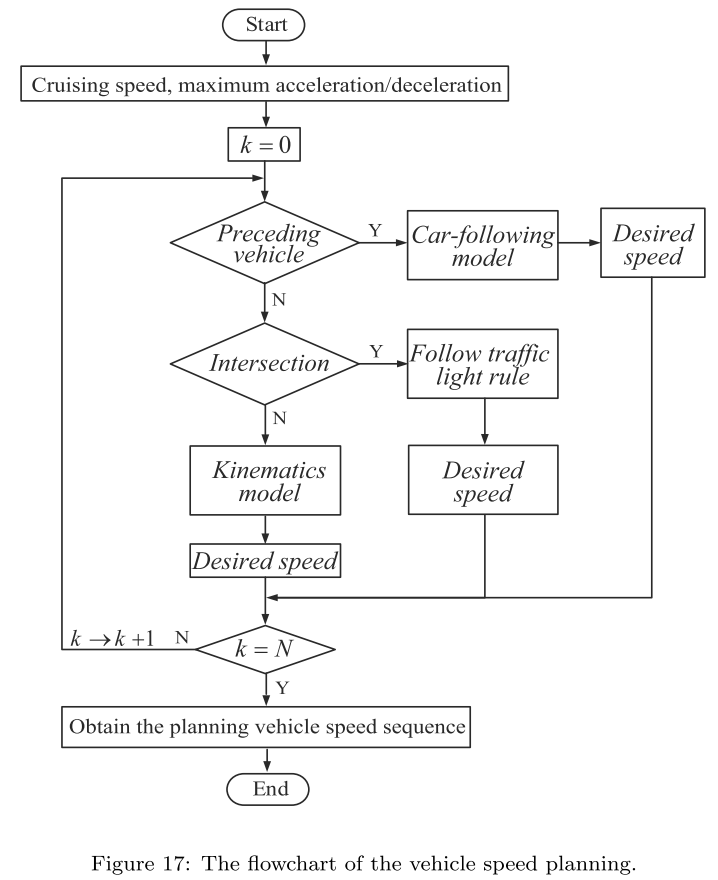
-
- PID:根据参考车速和实际车速控制demand torque(最终输出给轮上的扭矩)。 motor torque可以由demand torque, engine torque, and generator torque计算而来。
- MPC进行energy management, 8 steps, 0.1s sampling time Energy managment:如何根据输入的demand torque选择应从电池输出/冲入能量在总输出中占比(即engine,motor和generator的工作状况)。 为了降低计算负担,只有当demand acceleration reaches a specific value的时候(即driver demand torque reaches a specific value)的时候才使用MPC
- 刹车:rule-based
Worst-case relative cost optimal control for dynamic systems with finite admissible disturbance sequence sets
Xiangrui Zeng et al., International Journal of Control, 2019, link
progress: 20%
主要工作
- 针对的系统:一类discrete-time nonlinear system with uncertainties 优化对象:relative cost(对于一部分系统,absolute optimal cost value可能极大程度上由disturbances决定) 保证最优性能guaranteed optimal performance 不追求绝对cost最低(由于上述原因,absolute optimal cost value由disturbances决定),考察relative cost。 relative cost: defined as the ratio of the actual cost and the posteriori optimal cost
- 解决方案:利用backward induction 进行求解 输入:current states,current accumulated cost和all current and past disturbance values
- 应用:如nonlinear electric vehicle energy management problem
系统模型
-
Linear system with quadratic cost
- 系统模型
- with a quadratic running cost:
- terminal cost
, N=10 - initial condition
- constraints:
and
- 系统模型
-
disturbance sequences初步的假设 结论:若所有可能的disturbance sequence都已知,每次都会对当前的disturbance进行测量,那么随着控制的持续,能与当前所有测量得到的disturbance序列匹配的可能序列就越来越少
是一个disturbance sequence , 包含了所有可能的disturbance sequence ,先验的,有限集(priori, finite set)。即 是由序列组成的集合。 ,用 对每个 进行索引indexing - 那么已知past disturbance sub-sequence
,这个sub-sequence可以和 中的某些序列匹配(即已经出现的 项和部分 序列的前 项一一对应),满足上述匹配条件的 的所有索引所组成的集合可记为 其中 表示索引为 的 序列中的第 个元素,即第 步 - 因为满足条件的序列将越来越少,直至最后
中只有唯一个编号为 的disturbance sequence能与之对应,所以随着 的增加, 是一个’shrinking’ set
disturbance sequences概率的引入
- 为每个
引入对应的 ,表示其出现概率,即与 对应的,有vector Deterministic情况下,当有若干个可能序列时,其各自机会均等。 Stochastic情况下,需根据 计算可能时某个序列的概率。 - As the disturbance is measured at each step, some disturbance sequences in the set
will become disqualified at certain steps. Therefore the knowledge of the vector needs to be updated at every step 由上述假设,可能与当前序列匹配的先验序列随着控制的持续越来越少,那么从当前序列是其中某个序列的概率在每一步都会变化
Backward induction
-
If
is not unique, any that satisfies these equations can be chosen
Optimal Speed Control of a Heavy-Duty Vehicle in the Presence of Traffic Lights
Manne Held et al., CDC 2018, link
Progress:
- Terms:
- HDV: Heavy-duty vehicle
主要工作:
- The formulation of the problem of minimizing the energy consumption of an HDV (heavy-duty vehicle) driving in the presence of traffic lights as a Quadratic program (QP)
- An algorithm to find the energy-optimal timing of passing the traffic lights when the vehicle is constrained by a minimum allowed velocity
系统模型:
- Vehicle model:
- Traffic light model
- 优化问题
- Cost function
状 态 转 移 - 约束条件
Kinetic energy上下界
$$
K_{l,j}\leq K_j\leq K_{u,j} \tag{10c}
F_{t,j}\leq a_1+a_2K_j \tag{10d}
g_{np}\leq\Delta s\sum\limits_{j=k}^n\phi_{0,j}+\phi_{1,j}K_j\leq r_npPassing the traffic lights at position index $n$ at green signal $$ - Cost function
Robust Optimal ECO-driving Control with Uncertain Traffic Signal Timing
Chao Sun, et al., ACC 2018, link
Progress: .
- Terms
- ICE: internal combustion engine (vehicle)内燃机
- IDM: Intelligent driver model
- SPaT: signal phase and timing
主要工作:
- Robust optimal eco-driving control strategy
系统模型
- 信号灯模型:
- Modified intelligent driver model
- 与前车的预期距离
- 与前车的预期距离
- 优化模型
- Cost function:
- State variables:
- Control variables:
- Physical constraints:
- Final arrival time and traffic signal passing constraints:
- Cost function:
Predictive Cruise Control: Utilizing Upcoming Traffic Signal Information for Improving Fuel Economy and reducing Trip Time
Behrang Asadi et al., IEEE trans on CST 2011, link
Progress: .
主要工作:
- 设计了一套ACC巡航控制,Control objective:
- 尽量减少刹车,到达路口时为绿灯timely arrival at green light with minimal use of braking
- 保持安全车距maintaining safe distance between vehicles
- 行驶速度尽可能接近巡航速度cruising at or near set speed
系统模型:
- 设定参考车速Reference veloctiy planning
- 策略:加快速度,在绿灯变红前通过红绿灯,或减慢速度,在红灯变绿后通过红绿灯,通过下一个绿灯的起始时间/终止时间与距离计算参考车速
- 进行plan时,将位置记为零点,时间记为0.
- 得到参考车速的情况下对速度轨迹进行跟踪Optimal Tracking of the Reference Velocity
- 对于第
- state-space discretized form:
- State vector:
- Control input:
- Measured disturbance:
- 由以下连续状态离散化而来
- state-space discretized form:
- Objectives
- 若总计预测
- Speed limit
- Engine
- brake force limits
- Minimum safe following distance
- 若总计预测
- 对于第
Cooperative Adaptive Cruise Control Applying Stochastic Linear Model Predictive Control Strategies
Dominik Moser et al., ECC 2015, link
progress:
主要工作:
系统模型:
- Stochastic velocity prediction
Observations showed that the first few seconds of the upcoming velocity of a vehicle are mainly dependent on the vehicle’s current dynamic state. However, for a longer prediction horizon, the upcoming traffic situation and the driver’s reaction on it has to be considered as well to obtain meaningful results with low uncertainty.
Model predictive control for hybrid vehicle ecological driving using traffic signal and road slope information
Kaijiang Yu et al., Control Theory Tech, 2015
Progress:
主要工作:
系统模型:
An energy driven road-to-driver assistance system for intersections
Matteo Corno et al., ECC 2015
Progress:
主要工作:
系统模型:
Globally energy-optimal speed planning for road vehicles on a given route
Xiangrui Zeng et al., Transportation Research, 2018 tags:#dp
Progress: 80%
主要工作:
- 已知的问题:在route上有多个traffic lights,stop signs,以及不同的road grade时,如何找到global optimal speed planning solution。解决这个问题的主要难度在于这个最优化问题的约束是在不同domain上进行描述的:
- 交通灯的位置,stop signs的位置和速度限制是通过distance domain进行描述
- 交通灯变化的时间表是通过time domain进行描述
- route information和features用于对车时速进行最优控制,但是往往分为two domains:distance-domain和time-domain,如何进行转化
系统模型:
- System dynamics and physical model
- 当
- 若在行驶过程中停车(车速不能为负)
- 当
- State dynamics and model:
- State vector
- Input
- system dynamic function:
- Minimize
- State vector
- Constraints:
- 起始状态
- 终止状态
- 加速度上下限
- 速度上限sl (speed limit),下限lower bound (lo)
- 前车车距(假设前车车速)
- 前车状态
- 保持车距:
- 如何将non-standard form constraints转化为standard-form:
- Stop sign constraint (st):
- 存在的问题:
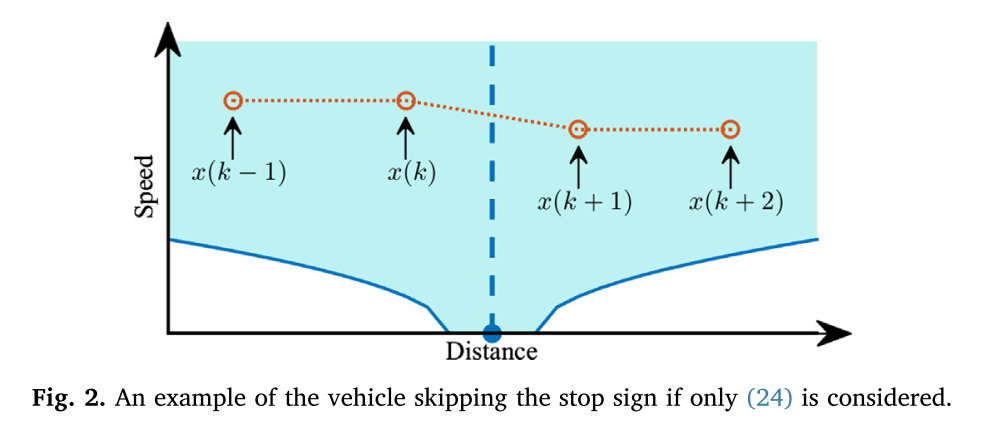 车辆在
车辆在 - 解决方案:
用
- 存在的问题:
- 交通灯 traffic lights,需要将时间加以考虑
- 转向 turns and curves
- Stop sign constraint (st):
- 前车状态
- An additional boolean state to improve driving comfort
- 起始状态
模型思路总结
-
元素间关系
System dynamics Corresponding state dynamics If eq(11) eq(5) eq(6) If eq(9) eq(10) Energy Cost function eq(7) eq(12) eq(8) Constraints Standard form Start state constraint eq(13) End state constraint eq(14) Acceleration constraint eq(15) Speed limitation eq(16) eq(17) Speed lower bound eq(18) eq(19) Safety distance eq(20) eq(22) eq(21) Traffic light eq(28) If eq(32)
eq(33)eq(29) If -
实现:将带有
- 速度上限,eq 16
- 因为在状态
- For
- 具体实现:在初始化
- 所以对于不同
- 因为在状态
- 速度下限,eq 18
- 因为在状态
- 具体实现:在初始化
- 因为在状态
- 安全车距,eq20/21二选一
- 因为在状态
- 具体实现:
- 因为在状态
- Stop sign, 为防止离散化后state
- 具体实现:
- 对于每一个
- 对于满足上述条件的
- 对于每一个
- 具体实现:
- Traffic light
- (注意和其它几篇论文的区别)这里没有假设红绿灯切换的period对于车辆是已知(即一般情况,车辆没有红绿灯在未来将变化的信息)。
- 参考stop sign的constraint
Eq 28: If
- When the traffic light is red, at the positions before the traffic light, the constraints are the same as a stop
- There is no constraint at the positions after the traffic light
- When the traffic light is green, it is considered as no constraint at all
- 为什么”there is no constraint at the positions after the traffic light”:因为前一状态与现状态之间可能存在red light,也有可能一直是green light
因此对于出现红灯时需要eq 28。
因为后一状态不关心前一状态是否为红灯(或者认为状态可以合并),因此对于
- 将stop sign constraints转化为有traffic light时对
- 当前状态是否为红灯?(一个额外的环境参数,true执行下一步,否则不需要constraint)
- 判断对于
- 用stop sign的constraint eq28进行判断
- 对于满足上述条件的
- 对于满足上述条件的
- 速度上限,eq 16
实验参数
- Sampling period: 2s
- Route discretization: 1m
The feasible state set is calculated numerically based on this grid,
- Speed discretization: 0.19m/s to 0.66m/s, denser in low speed, sparser in high speed.
- At each step, no more than 61 valid inputs will be searched。