matrix_overview

Matrix §

1. 行列式determinant §

• 代数意义：
• 几何意义：n维上的体积。 The determinant gives the signed n-dimensional volume of this parallelotope. e.g.(from wiki): , . . The volume of the purple area is:
  
• 负的行列式意味着将面积/体积反转过来（想象一张平行四边形纸片正面的面积为正，反面的面积为负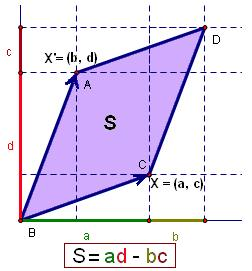） 图片来自维基

2. 特征值和特征向量eigen value and eigen vector §

• 参考知乎
• 假设有矩阵。由可以求出其特征值为，。
• 若，可解出，可见其为一系列向量，均指向同一方向。同样，对于，其对应的特征向量为。
• 也就是将矩阵所对应的旋转，拉伸，错切（二维空间上，二阶矩阵不能实现平移，三阶才可以）应用在特征向量上时，其作用与这个向量乘以对应的特征值相同，即只实现了拉伸。（特征向量和新的/映射后空间中的单位向量是什么关系呢？）
  旧坐标系中的被映射到了；旧坐标系中的被映射到了 新的坐标系中的为旧坐标系中的；新的坐标系中的为旧坐标系中的。
• 在利用进行旋转拉伸的过程中，特征向量所在的直线没有发生任何旋转，其他从原点发出的向量（不考虑平移）都因为投影发生了旋转。下面两个图表现了用进行变换后的效果。黑色箭头的起点和原点的连线为一个向量，箭头表示了在与相乘之后是如何变化的（与原向量的差的方向，箭头的长度经过了归一化，所以在这里比实际的短）。右侧的梯度图表示变换后的向量长度变化的系数（）。可以看到所有向量都朝着同一个方向（正负）旋转，其中一个特征向量对应的是这个方向（绿线），另一个特征向量是与其两侧的方向（红线，此例中不正交）。同时对于两个方向，每个方向上向量的模的变化比例是相同的 （用绿线和红线标出），和特征值的绝对值相同，是在曲面上的两条直线。（如果一个以z轴为转动轴的平面扫过，与曲面相交的结果是怎样？）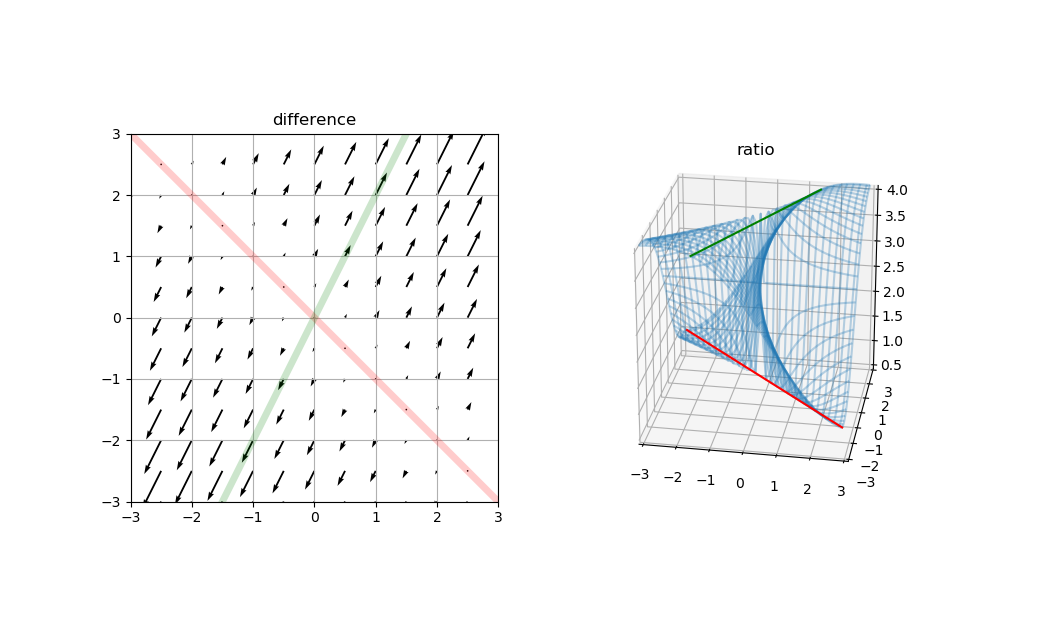
• 对，，对，。均不再满秩（同样， 行列式变为0）。特征值与单位矩阵相乘可以帮助去掉组成矩阵中的一组基，使其不再满秩。
• 特征值相当于把矩阵所有在原本的基上的拉伸提取了出来，（和相应的旋转/翻转（特征向量）作用之后就可以回复出原矩阵？但是特征向量组成的矩阵秩不为1，说明不是单纯的旋转一类的运动？）。（虚数特征值呢？如何理解旋转？知乎）
• 如果矩阵是呢？（MIT OCW）
• 行列式为特征值之积，迹trace为特征值之和
• 令，，可得，故有
• 与SVD的区别：特征值不一定正交，SVD要找到正交基

3. 齐次多项式，二次型与正定 §

• 二次型：n个变量上的二次齐次多项式（每一项均为二次，或），设法将其变换成标准型（只含平方项）
  令， 则

  • 几何意义：抛物线，抛物面，etc. （方便寻找极值点，从而变为最优化问题）

• 正定：，对，都有（），则为正定二次型，是正定的。 若，则是半正定的。

• 多维高斯分布的协方差矩阵是半正定矩阵。 特例：个高斯分布均独立不相关

• , 其中 ，协方差矩阵

• 对称矩阵的二次型求导

矩阵求导 §

• https://zhuanlan.zhihu.com/p/288541909

4. Jacobian and Hessian雅可比和海森矩阵 §

• Jacobian：一阶偏导
  • For a multi-link arm, ， where , the vector of input of joints ( or ).
• Hessain：二阶偏导，用于多元函数极值的判定

5. 合同变换 §

• 待整理1，2