Z's learning note

Search

SearchSearch

parallel_reduction

Dec 14, 2020, 18 min read

Parallel Reduction

参考nvidia: optimizing parallel reduction in CUDA

优化的核心问题

  • Parallel reduction优化的核心之一是减小同一个warp内部的线程差异化，因此在kernel初始化时或在global memory初始化时就应将数据补齐至2的次幂且大于等于32（补0或其他相应值），在计算过程中尽量避免可能在一个warp内导致不同走向的三元操作符和条件判断生效，所有操作尽量以32个连续threads作为最小单位。

  • shared memory的初始化（extern关键字，传入gridSize, blockSize和sizeof(var)*smemSize）： 若动态声明shared memory，初始化时检查越界 (以下代码未检查越界)

    • sdata[tid] = g_idata[i]; sdata[tid] = g_idata[i]+g_idata[i+blockDim.x]; 可能出现越界
    • sdata[tid] = (i < n)?g_idata[i]:0; if (i + blockSize < n) sdata[tid] += g_idata[i + blockSize]; 会将越界后的置为0

  • 以下代码应用时应补全边界检查部分。

优化1与2：减小warp内部线程间的差异，替换求余”%“运算符

  • Reduction 1： 通过判断thread ID是否是2的指数的整数倍，选择是否进行运算 在一个warp内，整个程序的执行过程中始终有部分thread执行if条件，部分执行else条件（从indexing的角度，间隔若干个，有一个工作），即divergent warps

  • Reduction 2： 通过在indexing时将其赋值为2的指数，跳过了剩余的theads，需判断index是否越界 在indexing靠前的warp内部，threads始终执行if分支，排在后面的warps/threads会随着迭代依次执行else条件

  • Highly divergent warps are very inefficient, and % operator is very slow

    • 注意图中线程的编号
Reduction 1Reduction 2
![[learning_note/1.theory/0.algorithm_basic/parallel_computing/zz.attachment/reduction1.png600]]
__global__ void reduce0(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;

sdata[tid] = g_idata[i];
__syncthreads();

for (unsigned int s = 1; s < blockDim.x; s *= 2)
{

    <font color="#dd0000">if (tid % (2 * s) == 0)
        sdata[tid] += sdata[tid + s];</font>
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}


__global__ void reduce1(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;

sdata[tid] = g_idata[i];
__syncthreads();

for (unsigned int s = 1; s < blockDim.x; s *= 2)
{
    <font color="#dd0000">int index = 2*s*tid;
    if (index < blockDim.x)
        sdata[index] += sdata[index + s];</font>
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}

优化3：shared memory bank冲突

  • Shared memory以4byte (32bit)为一个bank，共32个bank（与warp内thread数对应），程序需经过bank再找到具体内存地址。若一个warp内有多个线程同时访问同一个bank的数据就会产生shared memory bank conflicts 同一个warp内线性寻址或者broadcast可以避免或减少此问题（实现起来也就是在kernel中线性寻址），间隔寻址（如reduction1/2）或者随机寻址可能会造成shared memory bank conflict

  • 通过Bank寻址可以下图为例，Ref: What is a bank conflict? (Doing Cuda/OpenCL programming)

    Bank123…
    Address00 01 02 0304 05 06 0708 09 10 11…
    Address64 65 66 6768 69 70 7172 73 74 75…
    …

  • Sequential addressing is conflict free

    避免一个warp内的threads同时访问临近bank（shared memory）

  • CUDA toolkit documentation中的配图Ref:I.4.3. Shared Memory

左、右无冲突，中间不同thread访问bank中不同数据，有冲突不同thread访问bank中相同数据，左、中、右均无冲突
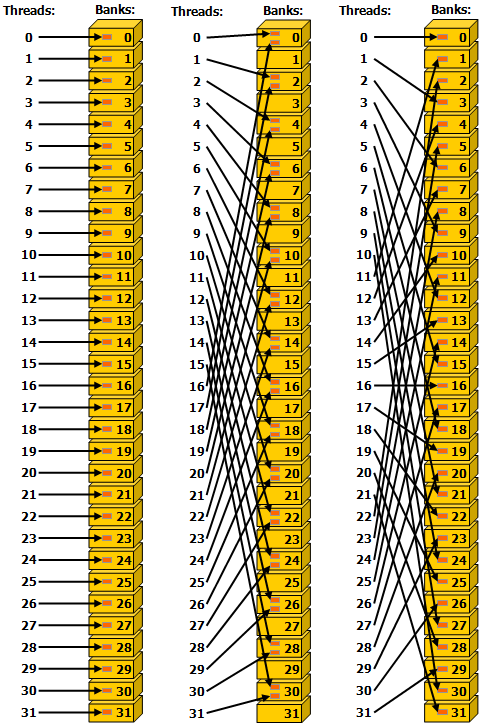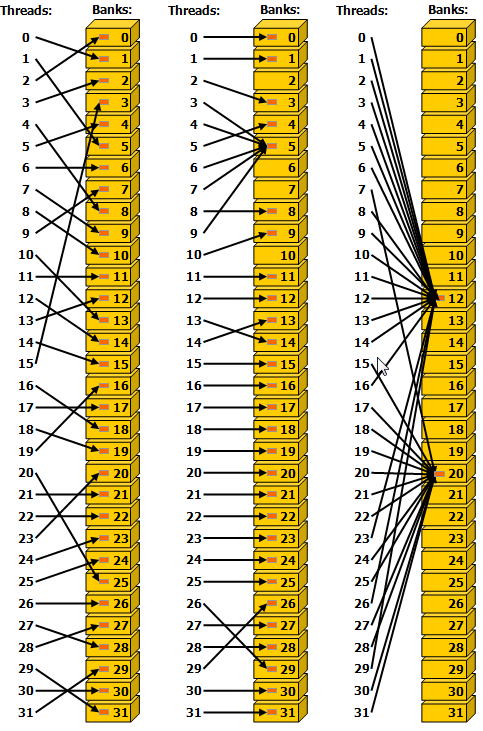Reduction 2Reduction 3
![[learning_note/1.theory/0.algorithm_basic/parallel_computing/zz.attachment/reduction2.png600]]
__global__ void reduce1(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;

sdata[tid] = g_idata[i];
__syncthreads();<br />
<font color="#dd0000">for (unsigned int s = 1; s < blockDim.x; s *= 2)
{
    int index = 2*s*tid;
    if (index < blockDim.x)</font>
        sdata[index] += sdata[index + s];
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}


__global__ void reduce2(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

    // each thread loads one element from global to shared mem
    unsigned int tid = threadIdx.x;
    unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;

    sdata[tid] = g_idata[i];
    __syncthreads();

<font color="#dd0000">for (unsigned int s = blockDim.x/2; s > 0; s >>=1)
{

    if (tid < s)</font>
        sdata[tid] += sdata[tid + s];
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}

优化4：初始化赋值时完成一次加法

  • 注意！：此时除了kernel函数需要修改，在启动kernel时传入的gridDim也需要进行相应的修改 因为在初始化时进行了一轮求和运算，因此block数可以减半，每个block内的threads数保持不变（即不需要改变循环中的初值s=blockDim.x/2） 例如：若同样启动512个threads，Reduction 1～3一个block只能用来计算512个数字之和，在第一个iteration之后停掉其中的一半，即有一半的thread只被用来初始化shared memory，从来没有用来计算。Reduction 4在初始化时每个thread先完成一次计算，即完成了1024->512，随后过程与Reduction 3一样，每次对半停掉thread。
Reduction 3Reduction 4
__global__ void reduce2(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
<font color="#dd0000">unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;

sdata[tid] = g_idata[i];</font>
__syncthreads();

for (unsigned int s = blockDim.x/2; s > 0; s >>=1)
{
    if (tid < s)
        sdata[tid] += sdata[tid + s];
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}


__global__ void reduce3(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
<font color="#dd0000">unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;

sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];</font>
__syncthreads();

for (unsigned int s = blockDim.x/2; s > 0; s >>=1)
{
    if (tid < s)
        sdata[tid] += sdata[tid+s];
    __syncthreads();
}

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}

优化5：部分循环展开

  • 计算的流程前半部分是一样的，当剩余需要计算的threads小于等于32个时，接下来的此时运算将集中在第一个warp中，序号为0~31的thread。为了避免这个warp内线程的差异化，将循环实现的折半求和运算展开为一个线程内的顺序（sequential）运算
  • warpReduce中的每一步对于这个warp中的每一个thread都是同步的，不需要额外的__syncthreads()。对于第一个warp省去了for循环中的位移，判断，及循环内部的同步。剩下的warp都将停止在if (tid < 32)
  • 注意保留device代码的volatile！编译时device代码将直接在kernel内部替换展开。
Reduction 4Reduction 5
未应用模板 
__device__ void warpReduce(volatile int* sdata, int tid)
{
    sdata[tid] += sdata[tid + 32];
    sdata[tid] += sdata[tid + 16];
    sdata[tid] += sdata[tid + 8];
    sdata[tid] += sdata[tid + 4];
    sdata[tid] += sdata[tid + 2];
    sdata[tid] += sdata[tid + 1];
}

__global__ void reduce3(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;

sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];
__syncthreads();

<font color="#dd0000">for (unsigned int s = blockDim.x/2; s > 0; s >>=1)</font>
{
    if (tid < s)
        sdata[tid] += sdata[tid+s];
    __syncthreads();
}


// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}


__global__ void reduce4(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

    // each thread loads one element from global to shared mem
    unsigned int tid = threadIdx.x;
    unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;

    sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];
    __syncthreads();

    for (unsigned int s = blockDim.x/2; s > 32; s >>=1)
    {
        if (tid < s)
            sdata[tid] += sdata[tid+s];
        __syncthreads();
    }
    if (tid < 32) warpReduce(sdata,tid);

// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}

优化6：使用c++模板从而展开全部循环

  • 表格中内容Reduction 6的红色部分将在编译时由编译器根据定义的每个block中thread的数量进行优化。 从而完成了将整个for循环完整的展开，避免循环中的判断、位移和同步
Reduction 5Reduction 6

__device__ void warpReduce(volatile int* sdata, int tid)
{
    sdata[tid] += sdata[tid + 32];
    sdata[tid] += sdata[tid + 16];
    sdata[tid] += sdata[tid + 8];
    sdata[tid] += sdata[tid + 4];
    sdata[tid] += sdata[tid + 2];
    sdata[tid] += sdata[tid + 1];
}

template <unsigned int blockSize>
__device__ void warpReduce5(volatile int* sdata, int tid)
{
    if (blockSize>=64) sdata[tid] += sdata[tid + 32];
    if (blockSize>=32) sdata[tid] += sdata[tid + 16];
    if (blockSize>=16) sdata[tid] += sdata[tid + 8];
    if (blockSize>= 8) sdata[tid] += sdata[tid + 4];
    if (blockSize>= 4) sdata[tid] += sdata[tid + 2];
    if (blockSize>= 2) sdata[tid] += sdata[tid + 1];
}


__global__ void reduce4(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

    // each thread loads one element from global to shared mem
    unsigned int tid = threadIdx.x;
    unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;

    sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];
    __syncthreads();

    for (unsigned int s = blockDim.x/2; s > 32; s >>=1)
    {
        if (tid < s)
            sdata[tid] += sdata[tid+s];
        __syncthreads();
    }



    if (tid < 32) warpReduce(sdata,tid);

    // write result for this block to global mem
    if (tid == 0)
        g_odata[blockIdx.x] = sdata[0];

}

template <unsigned int blockSize>
__global__ void reduce5(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

    // each thread loads one element from global to shared mem
    unsigned int tid = threadIdx.x;
    unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;

    sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];
    __syncthreads();

    if (blockSize >= 1024){
        if (tid < 512) {sdata[tid] += sdata[tid+512];} __syncthreads();}
    if (blockSize >= 512){
        if (tid < 256) {sdata[tid] += sdata[tid+256];} __syncthreads();}
    if (blockSize >= 256){
        if (tid < 128) {sdata[tid] += sdata[tid+128];} __syncthreads();}
    if (blockSize >= 128){
        if (tid < 64) {sdata[tid] += sdata[tid+64];} __syncthreads();}

     if (tid < 32) warpReduce5<blockSize>(sdata,tid);

    // write result for this block to global mem
    if (tid == 0)
        g_odata[blockIdx.x] = sdata[0];

}
主函数调用kernel 
reduce4<<< blocks/2, threads, smem_size>>>(g_odata, g_idata, n);


用以下条件选择替换主函数中对kernel的调用。(调用时blocks要注意是否需要除以2)

switch(threads)
{
    case 1024:
        reduce5<1024><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 512:
        reduce5< 512><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 256:
        reduce5< 256><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 128:
        reduce5< 128><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 64:
        reduce5<  64><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 32:
        reduce5<  32><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 16:
        reduce5<  16><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 8:
        reduce5<   8><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 4:
        reduce5<   4><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 2:
        reduce5<   2><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
    case 1:
        reduce5<   1><<< blocks, threads, smem_size>>>(g_odata, g_idata, n);
        break;
}





优化7：级联（algorithm cascading）


    

  • 

    基于Brent’s Theorem, Ref:  Overview, Models of Computation, Brent’s Theorem
并行运算的复杂度由必须串行（前后相互依赖的计算）的复杂度和无依赖关系的计算并行后的复杂度共同决定
    

    • 

  • 

    需要对number of blocks和number of threads进行试验才能得到应为kernel配置的值。
    

    • 

  • 

    在RTX2070运行结果如下（单位：us）

    

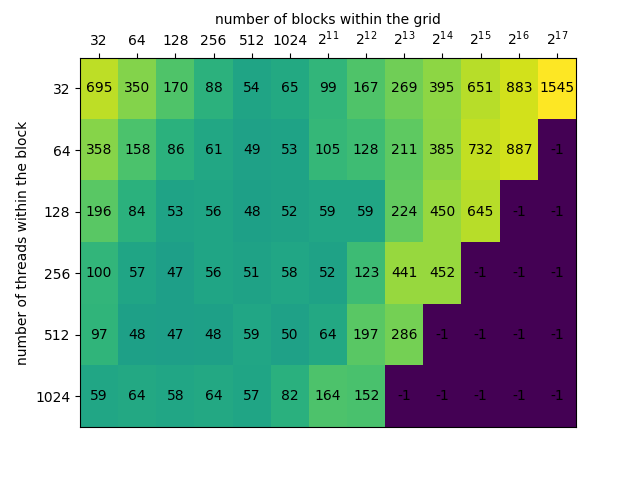
    若将计算完全并行化，若尽可能多的配置，需要将kernel配置为<<<4096,1024>>>，耗时约为100us
可以看出blocks应配置在128～1024之间，threads应配置在256～1024之间，耗时大约为上面的一半
    

    • 



Reduction 6Reduction 7


template <unsigned int blockSize>
__global__ void reduce5(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;




<font color="#dd0000">sdata[tid] = g_idata[i]+g_idata[i+blockDim.x];</font>
__syncthreads();<br />
if (blockSize >= 1024){
    if (tid < 512) {sdata[tid] += sdata[tid+512];} __syncthreads();}
if (blockSize >= 512){
    if (tid < 256) {sdata[tid] += sdata[tid+256];} __syncthreads();}
if (blockSize >= 256){
    if (tid < 128) {sdata[tid] += sdata[tid+128];} __syncthreads();}
if (blockSize >= 128){
    if (tid < 64) {sdata[tid] += sdata[tid+64];} __syncthreads();}
	
 if (tid &lt; 32) warpReduce&lt;blockSize>(sdata,tid);
 
// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];
	



}




template <unsigned int blockSize>
__global__ void reduce6(int* g_odata, int* g_idata, int n)
{
    extern __shared__ int sdata[];

// each thread loads one element from global to shared mem
unsigned int tid = threadIdx.x;
unsigned int i = blockIdx.x*(blockDim.x*2) + tid;
<font color="#dd0000">unsigned int gridSize = blockSize*2*gridDim.x;
sdata[tid]=0;

while (i < n)
{sdata[tid] += g_idata[i]+g_idata[i+blockDim.x]; i+= gridSize;}</font>
__syncthreads();<br />
if (blockSize >= 1024){
    if (tid < 512) {sdata[tid] += sdata[tid+512];} __syncthreads();}
if (blockSize >= 512){
    if (tid < 256) {sdata[tid] += sdata[tid+256];} __syncthreads();}
if (blockSize >= 256){
    if (tid < 128) {sdata[tid] += sdata[tid+128];} __syncthreads();}
if (blockSize >= 128){
    if (tid < 64) {sdata[tid] += sdata[tid+64];} __syncthreads();}
	
if (tid < 32) warpReduce6&lt;blockSize>(sdata,tid);<br />
// write result for this block to global mem
if (tid == 0)
    g_odata[blockIdx.x] = sdata[0];<br />



}




在调用kernel前配置：

int blocksize = 1024;
int gridsize = (len+blocksize-1)/blocksize;



在调用kernel前配置：

int blocksize = 256;
int gridsize = 256;





实现与测试


函数实现


    

  • Slides中数据类型为int，填充shared memory时不做越界检查。
    • 

  • 官方实现在“6_Advanced/reduction”文件夹中
    • 

  • 官方实现中的数据类型采用了template，支持的数据类型为int，float和double

      

    • C++中int为4 byte（-2^31~2^31-1），测试求和时最大元素不应超过1<<15，否则累积和会超过int最大值
      • 

    • 测试时尽量避免使用浮点数进行测试，如果用GPU将数据分组相加，再将几组数据用CPU进行求和，可能会因为浮点数精度问题造成误差（如果数量很大，如6k个数相加）
对此问题的具体测试方法：将整数替换为浮点数，计算，大约会在5000~6000之间出现明显的误差（出现在n=5795时，blockDim=<1024>，gridDim=<6>，用GPU求得block内的总和后用CPU对6个分组的和再进行求和，CPU与GPU误差为2）
      • 

    

    • 



将问题分层处理


    

  • 

    Slides第5页提供的建议：递归调用kernel（实现参考Ref: Dynamic parallelism in CUDA）
    

    

    Recursive kernel invocation
    

    

    但是在slides中展示的kernel代码并不包含递归部分
    

    • 

  • 

    官方例程的处理办法：迭代
在待求和的元素数量大于cpuFinalThreshold时，每次重新计算block和thread数，将d_odata拷入d_intermediatesum作为新的输入，再调用kernel。
    

    while (s > cpuFinalThreshold) {
	int threads = 0, blocks = 0;
	getNumBlocksAndThreads(kernel, s, maxBlocks, maxThreads, blocks,
						   threads);
	checkCudaErrors(cudaMemcpy(d_intermediateSums, d_odata, s * sizeof(T),
							   cudaMemcpyDeviceToDevice));
	reduce<T>(s, threads, blocks, kernel, d_intermediateSums, d_odata);
 
	if (kernel < 3) {
	  s = (s + threads - 1) / threads;
	} else {
	  s = (s + (threads * 2 - 1)) / (threads * 2);
	}
  }
    

    • 



测试参数与方法


    

  • Slides中提到的测试参数：


    • 

  • 官方示例

      

    • 使用了cuda-samples/Common/helper_timer.h中的sdkCreateTimer，sdkStartTimer和sdkStopTimer
      • 

    

    • 

  • 其它方式：cudaEvent

      

    • cudaEventCreate(&start)
      • 

    • cudaEventCreate(&stop)
      • 

    • cudaEventRecord(start, 0);
      • 

    • cudaEventRecord(stop, 0);
      • 

    • cudaEventSynchronize(stop);
      • 

    • cudaEventElapsedTime(&time, start, stop);
      • 

    

    • 

  • 采用系统计时应在cudaDeviceSynchronize()后再停止计时，否则只计入了kernel启动时间
    • 



测试结果


    

  • 

    电脑配置：CPU i5-6600K，内存 32GB @ 2133Mhz，显卡RTX 2070 8GB
    

    • 

  • 

    结果
    














































































    MethodTimestep
    speed up    		cumulative
    speed up    		ref step
    speed up    		ref cumulative
    speed up
    CPU0.010060 s
    Reduction 10.000734 sstandard
    Reduction 20.000486 s1.51x1.51x2.33x2.33x
    Reduction 30.000261 s1.86x2.81x2.01x4.68x
    Reduction 40.000152 s1.72x4.83x1.78x8.34x
    Reduction 50.000120 s1.27x6.12x1.8x15.01x
    Reduction 60.000115 s1.04x6.38x1.41x21.16x
    Reduction 70.000059 s1.95x12.44x1.42x30.04x
    

    • 

Backlinks