poe

PoE/Twist 旋量法 §

理论：从Twist的角度看待screw §

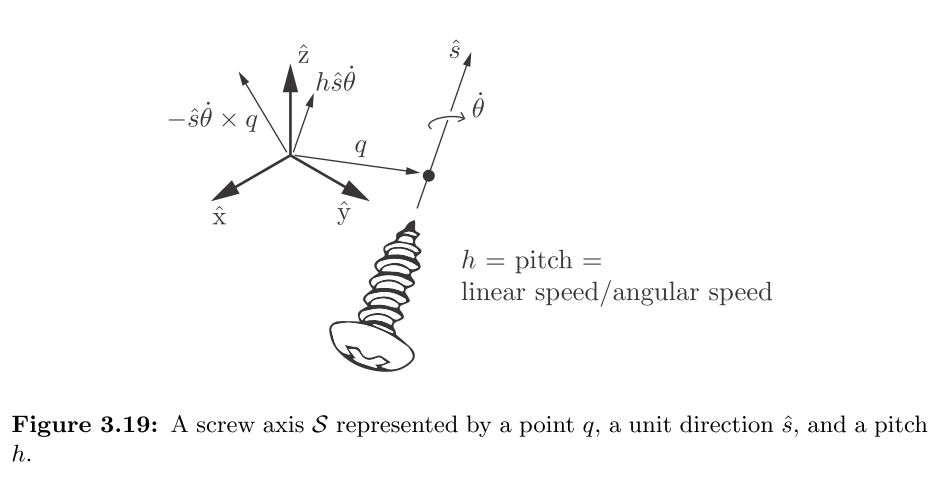
• 从物理性质的角度，想象将一枚螺丝拧到墙里（Modern Robotics, Lynch and Park）：
  1. 一个质点，即所示原点，所关心的运动发生的点
  2. 单位向量用于表征旋转在空间中的方向（螺丝钉轴线）
  3. 旋转轴上的点 ，建立一个平面，垂直于旋转轴，并且质点在该平面上。这个平面与旋转轴交于。
  4. 螺距，线速度与角速度的比值（一枚螺丝拧一定角度，对应的可以往墙里钻多深？），之后需要对是有限的值或者无限大分情况讨论
  5. 角速度，即假想中的螺栓旋转的速度
• 上述组成中变量为，固有构成为，和，为三维，质点到为二维（在和定义的平面上），为标量，总计六个维度，所以用它进行变换后得到的定义也应当为六个维度 并不采用，和直接定义screw axis
• 物理意义，表征一般化的运动：
  • 质心一边绕着一根轴旋转（找出物体绕着一个什么样的轴在进行运动）
  • 从质心画一条垂线到轴，交于点，以一定线速度在前进，这个前进的速度即为
• 定义Screw axis，建立一个参照系，原点为质心，坐标系为。screw axis 所表明的运动分为两种形式：
  1. ：当时的参照系的角速度，即螺线转轴的旋转是如何体现在参照系的每个轴上的 有两种情况，或为单位向量（将进行分解），或为（无旋转）
  2. ：当时参照系原点的线速度（三维的平移）。其模可以为任意值（？），每个方向上代表线速度的比例。它又由两部分组成：
     1. ：参照系原点所在平面（垂直于）的线性运动（也就是的线性运动）
     2. ：参照系本身旋转所带来的线性运动 中负号的由来： 图中的坐标系时绕着轴旋转的。的方向是由参照系原点垂直指向轴（交于黑点）。考虑由角速度计算线速度的公式中由圆心指向圆弧，与反向，因此需要加上负号。
• 针对分情况讨论（等价于讨论两种不同作为被除数对的影响）：
  1. 旋转轴为单位向量 存在旋转时 为有限的数值： 通过，，合成出的旋转方向（通过一根转轴表示），类比于三维的运动合成一个方向向量。 由于存在旋转运动，只要半径存在一定会导致位移，因此即使为0时也存在平移运动，即运动包含rotation和translation
  2. 当时 无旋转运动 为无限大 人为规定 ，即为单位向量，此时仅存在平移运动，用于将运动分解到各个轴向（定义screw axis的目的即使将，，进行转化，从而更好的表达为无穷大的情况）
• 也就是对于归一化的screw axis ，两者其一必须为单位向量（或为1）
• 将上面的坐标轴与相乘（中假定为1了），得到Twist：
• 一些情况可能会对normalized screw axis 和一般性的混用 和（Modern Robotics, Lynch and Park）

  Important: Although we use the pair for both a normalized screw axis (where one of or must be unity) and a general twist (where there are no constraints on and ), the meaning should be clear from the context

其它 §

• Adjoint transformation的物理意义：
  • 将twist从一个frame中变换至另一个frame

实际：应用screw axis/matrix §

应用方法 §

• 注：此处，，与混用
• 由原点至末端执行器，，需要找出的参量为home configuration 和 输入变量为关节，即角度（转动关节）或位移（线性关节）
• 那么需要找出与 与二者必有其一为单位向量，根据转轴类型分情况讨论
  • 旋转轴：
    • ，指明旋转轴的指向
    • 在中无平动，只考察的部分
      • 由给出
      • 为所在的轴（直线）到原点的距离，而不是所在的frame的原点到世界坐标原点的距离
  • 平动轴：
    • ，无旋转
    • ，用世界坐标系指明平动轴方向
• 找出home configuration 为最后一个坐标系在关节默认位置状态下相对于世界坐标系原点的transformation（原点指向末端点）

Toy problem §

实机应用 §