plan_w_preference

（文献综述）Planning with preference §

Jorge A. Baier et al., AI 2008

• Progress: 20%, link

• Terms:

• Preference-based planning (PBP)

• 主要调研了两个问题：

  1. 如何在PBP的框架下定义preference。（planning preference languages） 需要一种语言来定义preference，建立起用户的preference和规划的preference的联系 1. 如何定义preferences 2. Aggregate不同的preference
  2. 定义了preference后，如何有效的优化出preferred plan。（algorithms for planning with preferences）

• 传统规划与PBP（如何以preference作为依据比较plan？）

  • ，状态，初始状态，目标()和算子（operators）
  • 传统方法： STRIPS，ADL，PDDL（主流方法）。
  • PBP：用以表示依据preference对plan的比较（， is at least preferred as plan ），更严格的用
  • 部分（partial）/全部（total）preference

• Preference languages and formalisms（如何定义）

  • 需要考虑的点：
    • 普适性（compact, not explicitly）
    • (Over states) referring to properties of a plan.
    • (Over actions) Additionally provide for preferences over actions occurrences, 以附加在action上为主，也会部分的附加在state上。
    • Quantitative or qualitative or both
      • Quantitative languages: solutions are associated with numeric values
        1. Decision-Theoretic Planning (DTP)
        2. Partial Satisfaction Planning (PSP)
        3. PDDL3 Linear temporal logic involves here.
      • Qualitative languages: 不需要依据任何数据进行定义
        1. Languages Based on Ranked Knowledge Bases（Languages based RKB）
        2. Conditional Preference Networks (CP nets, Boutilier et al.) 扩展形式，引入了trade-offs：TCP-nets
        3. Temporal and Temporally Extended Preferences
      • Both：
        • 其它方法LLP，DT-Golog
  • 最近的解决方案PDDL3，planning with hierarchical task networks (HTN)

• PBP算法（如何求解）

  • Optimal, k-optimal, Incremental
  • Search-Based PBP
    • P_REF-S_EARCH
  • Final State Preferences
  • Temporally Extended Preferences (TEPs)
    • PP_LAN
    • HP_LAN-P
    • SGPlan₅
  • PBP through general-purpose solvers

• 研究方向

  • 效率问题。现在的PBP planner的效率主要依赖于relaxed planning graph techniques，在简单场景中信息不足（？）
  • 现阶段主要研究集中在detereminstic planning上。缺少对incomplete knowledge等情景的研究
  • 现阶段的解法需要preference elicitation已解决，但这点在实际问题中较难达成。以decision-making的形式获取user preference比较困难。一种解决的方向是用交互的方式develop a most-preferred plan。

A prior preference-based decision-making algorithm in Pareto Optimization §

Masoumeh Jafari et al., ICCKE 2019

• Progress: 20%, link

• 主要工作

  1. 对于multi-objective optimization（MOO）问题： 将objectives用Favorite Region（FR）表达，引入Angle-based updating Pareto front (PF) 算法中
     • FR（Favorite Region）基于objective space创建（将FR和angle-based引入PF问题）
     • PF的解在演进的过程中趋近于FR（要优化的会变得更好，不重要的也不会丢掉）
     • 不在FR中的解也不会消失（go away）。解的fronts level（？）会随着变化？
     • 如何平衡了适当的解的exploration和exploitation（均匀分布）？undesirable region中的解的密度也未受影响
  2. 实验

  问题： PF是什么？FR是什么？angle-based是什么？first and second frtons是什么？

  • Pareto optimal solutions：不是单一最优全局解，而是一组trade-off解（Pareto optimal set）
    • Pareto optimal set’s image of the objective space is Pareto optimal front
    • E.g.:
      • f1, f2: objectives space
      • non-dominance solutions sorted in first, second Pareto front
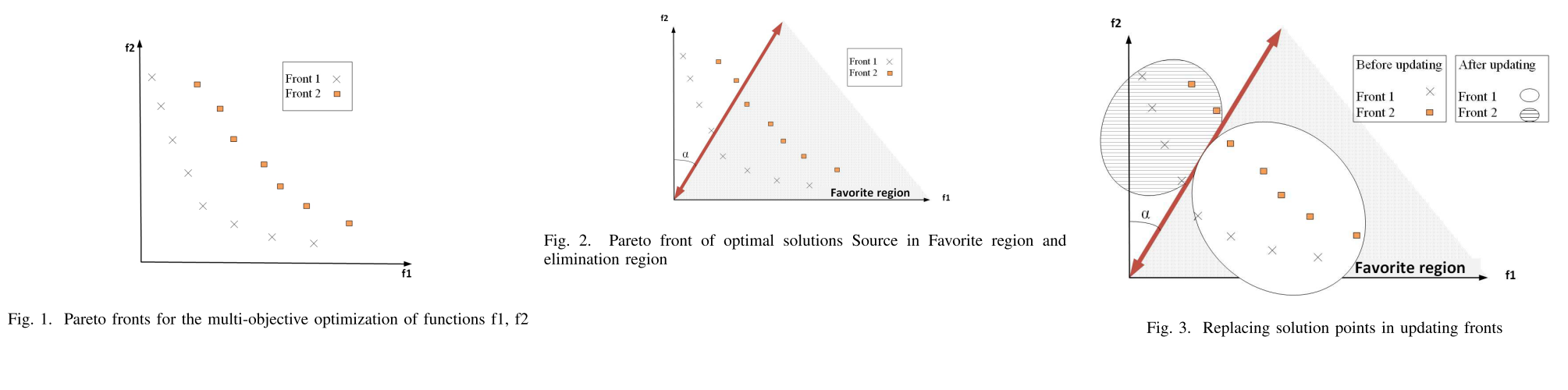
    • Decision making（DM） 两类MOO算法：No-preference和Preference-based 三种方法利用preference：（前两个是什么？最后一个好理解） 1. Priori method 2. Posteriori method（本文重点） 3. Interactively method

• Method:

  1. 旋转向量将Front 1 和Front 2进行划分
  2. 划分区域即为favorite region和elimination region
  3. 根据向量划分结果将favorite region内的解放入Front 1中，将elimination region中的解放入Front 2中
  4. 重复上述过程直至收敛或停止条件

• ref

  • 前置？A preference-based evolutionary algorithm for multiobjective optimization