coordinate

坐标系的变换 §

符号定义 §

• 约定：表示以0作为参照系，1的旋转变换（也记作） 齐次变换，记作, object transformation with respect to reference frame 对于机器人系统而言，是以父连杆（或机器人基座）作为参照系，子连杆相对其的变换 编程时变量形式的约定r_obj2ref（只包含旋转变换），ht_obj2ref（homogeneous transformation） 例：

旋转矩阵与齐次变换矩阵 §

• 以、、为轴的旋转矩阵的表示

矩阵的左乘与右乘 §

结论 §

• 以固定坐标系作为参照系进行旋转（如ROS的sxyz），矩阵左乘
• 以活动坐标系作为参照系（或者说在当前的基础上）进行旋转，矩阵右乘
• 图例

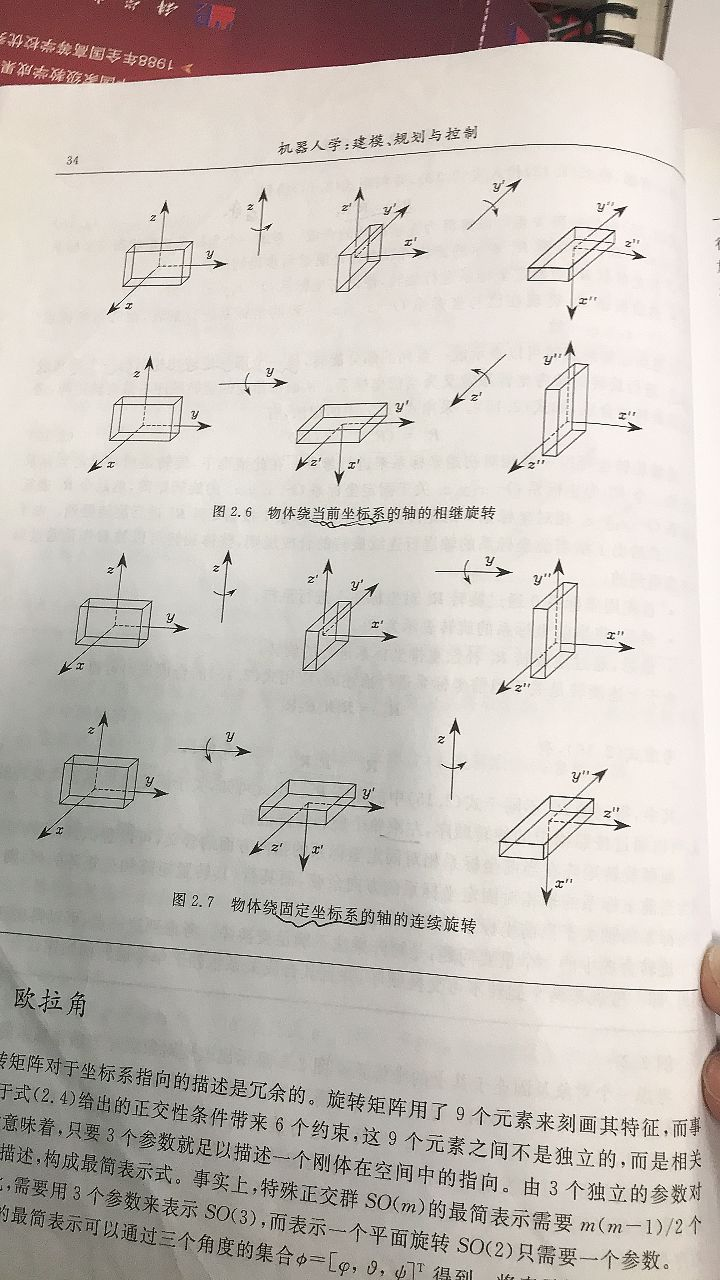
直觉 §

1. 直觉1
   • 假设从世界坐标出发，，旋转效果由位于左侧的矩阵产生，作用在右侧的矩阵/向量上（通过直觉不严格的证明：在变换一个列向量时，旋转矩阵应在其左侧），计算时总是从出发，与其最近的矩阵结合进行运算。
   • 计算时，先计算，即被旋转，然后运算结果再被旋转。第n步的旋转矩阵为，以世界坐标系为基准。
   • 计算时，先计算，即被旋转，那么此时变换矩阵的参照已改变（当前坐标系），运算结果再去旋转。第n步中新的旋转矩阵为，以最新的参照系作为基准，对进行旋转
2. 直觉2

• 齐次变换矩阵包含两个部分，旋转与平移，其形式又可等价的表示为

  • 计算时，考虑，根据运算律，先与结合进行运算（受到旋转影响）。平移未受到旋转的影响（以固定座标系作为基准）。最终结果为

  • 计算时，考虑，根据运算律，先与结合进行运算（产生旋转作用的是中的，即未被旋转，被旋转）。平移受到旋转的影响，由于此时已经在新坐标系下，平移需要回溯的影响（即，以新坐标系为基准）。最终结果为

理论 §

实践 §

正向运动学 §

• 在前向运动学中，从机器人的底座开始，下一连杆（子连杆）都是以上一连杆（父连杆）的坐标系为基准进行变换的计算，矩阵右乘：
• 同理在使用DH参数进行计算的过程中，如果用标准形式定义DH参数，也是先轴，再轴？

手眼校准 §

• 假设相机设置为正对机械臂，机械臂上粘贴有二维码，且二维码相对于机械臂基座的位姿已知（，ht_tag2world）。通过二维码识别可以获得（）二维码相对于相机的位姿（参考使用OpenCV检出二维码位姿），则相机相对于基座的位姿为。若要计算空间中某一点在成像平面上的位置（对应像素点），如基座（假设其为世界原点），则须进行一次变换，再投影至二维成像平面。

ht_cam2world = np.dot(ht_tag2world, np.linalg.inv(ht_tag2cam))
origin = np.dot(np.linalg.inv(ht_cam2world), np.identity(4))
px = proj_to_2d(k, origin[0:3,3])

欧拉角 §

俯仰角旋转 §

• 滚转俯仰有两种解释方式，先定义三个转角
  • Roll：以轴为轴向， Pitch：以轴为轴向， Yaw：以轴为轴向，
• 两种计算方式
  • Yaw-pitch-roll（旋转次序为，以固定坐标系为基准）
  • Roll-pitch-yaw
    • 每次旋转以上一次旋转后产生的当前坐标系作为基准进行旋转 先以轴作为旋转轴进行旋转 在旋转后的坐标系下以新的轴作为旋转轴 在再次旋转后的坐标系下以新的轴作为旋转轴
• 两者的变换均可以表示为