gpu_and_dp

Use GPU to accelerate solving dynamic programming §

---

优化的层级 §

• 分类：

  Level	Summary	Paper	Detail
  High-level	from the algorithm aspect	2016: [[learning_note/0.paper/gpu/gpu_and_dp#dynamic-programming-parallelization-of-matrix-chain-multiplication-on-gpu-a-comparative-study	Dynamic programming parallelization of matrix chain multiplication on GPU: a comparative study]]
  		2019: [[learning_note/0.paper/gpu/gpu_and_dp#a-cuda-approach-to-compute-perishable-inventory-control-policies-using-value-iteration	A CUDA approach to compute perishable inventory control policies using value iteration]]
  Mid-level	Computation-data access	2009: [[learning_note/0.paper/gpu/gpu_and_dp#on-the-robust-mapping-of-dynamic-programming-onto-a-graphics-processing-unit	On the robust mapping of dynamic programming onto a graphics processing unit]]
  Low-level	How it is run on specific HW

• High-level：将循环中前后项无相互依赖关系的序列运算并行化，将N -> 1

• Mid-level：在准备数据时进行padding等操作，提高内存效率

---

An efficient parallelization strategy for dynamic programming on GPU §

Karl-Eduard Berger et al., IPDPS 2013

• progress: 60%, link
• Terms:
  • MKP: multidimensional knapsack problem

主要工作 §

• 提出了一种为在CUDA上运行dynamic programming优化的thread grouping的并行策略
  • Dynamic programming对于计算的特点： naturally exposes an important level of parallelism, but also requires frequent synchronization between the parallel processes. 有大量需要并行计算的部分，同时又时常需要在并行进程间进行同步
  • 如何普适的在GPU进行DP，并提升并行效率
• 在背包问题（knapsack problem）上进行了验证 串行算法共两层循环，inner和outer
• 主要瓶颈necessary synchronization，解决方案：
  • 决定并行策略时需考虑到GPU的技术指标（通过API获取GPU参数）

从串行到并行 §

• sequencial MKP算法
• 在GPU上的并行实现
• GPU并行程度：fine, coarse,
  1. Fine grained strategy: 根据independent parallel operations数量，尽可能多的启用threads。对于MKP问题，将inner循环完全交由GPU并行化，outer循环由CPU控制。两者之间需要进行全局同步
  2. （未命名）将完整的KP算法在GPU kernel中实现 不同的blocks执行outer loop 在每次inner loop的iteration之后执行一次同步，因为CUDA不支持block之间同步（只有全局同步） 尽可能少的创建blocks，每个block包含尽可能多的threads（1024）
  3. Coarse strategy: 每个threads中执行若干inner loop的iterations，从而避免thead synchronization（论文剩下的部分采用的都是这种并行策略）
• 除了fine/coarse strategy，对内存进行coalesced memory access
• 有的paper报告texture memory access能提高性能，但是经过测试对这个问题没有影响，因
• 此没有使用texture memory
• 在Array中的数据索引：dynamic/static management of multiple constraints
  • 给定一个矩阵维度，和一个向量，如何求出向量对应的一维indexing。或反之，给定一个一维indexing，如何找出其在矩阵中的位置。
  • Dynamic management of multiple constraints: 方法：求模（mod） 缺陷：所有数据都需要存储在GPU global memory中
  • Static dimension specialization Fix the dimension of the problem（因为大多数工程问题的维度是固定的） 将item data (weights and profit)和背包容量保存为local variables 进一步提升：lighter computation of indeces，避免使用除法和求余运算进行索引

评价方法 §

• 3种不同平台组合，CPU+GPU（GPU的number of cores和streaming multiprocessors） CPU代码采用GCC编译，-O3级别优化 10种问题规模(10k，20k，…，100k instance)
• CPU用时；GPU fine方法（传统方法）用时，加速比例（CPU time/GPU time）；GPU coarse方法用时，加速比例（CPU time/GPU time）；fine与coarse的加速比例（fine time/coarse time）

结论： §

• Coarse比fine好，light比static好，static比dynamic好

---

A dynamic programming model to solve optimisation problems using GPUs §

Jonathan Francis O’Connell, Ph.D. thesis 2017

• link

主要工作 §

• 并行dynamic programming based model。同时运行GPU based computations和memory transactions。使得求解大规模问题时不会因为memory constraints导致运算暂停

---

GPU-accelerated value iteration for the computation of reachability probabilities in MDPs §

Zhimin Wu et al., ECAI 2016

-progress: 80%, link

主要工作 §

• 通过针对MDP代数特征的研究（algebraic features, e.g., matrix structure），通过action-based矩阵进行大规模并行以提高效率，比传统VI提升了10倍以上的速度，在绝大多数情况下比TVI（topological value iteration）表现好。
  1. Take advantage of the algebraic structure of MDPs to define action-based matrices and corresponding data structures for efficient parallel computation of reachability porbabilities on GPUs.
  2. Develop an efficient parallel VI algorithm for computing rechability probabilities that utilizes features of modern GPUs, e.g., dynamic paralleism and memory hierarchy.

Terms §

• TVI: topological value iteration
• SCCs: strongly connected components

解决方案 §

• Action-based matrices: 给出任意一个action，找出所有能使用这个action的state 以及在使用这个action之后后续所转移到的状态，和状态转移概率一起组成一个这个action所对应的新的矩阵 例如在Frozen lake中，action“向上走”中的是所有grids，是除掉底部的所有grids，顶部的设置为0；或者是去掉顶部的所有grids，是除掉底部的所有grids MDP: for each action , an action-based matrix is a tuple is the set of states in which action is activated is the se of states reached via action from states in
• 并行化：将action-based matrices作为最小单位，将整个过程转化为several interleaving action-based matrix to vector multiplications and subsequent minimisation where each action-based matrix to vector multiplication is an independent computation

实现与试验结果 §

• 与传统VI和TVI在五种数据集上进行了比较（数据集参见一作的Ph.D. thesis），主要考察整体运行时间。

其它 §

• 一作的Ph.D. thesis：Parallelizing Model Checking Algorithms Using Multi-core and Many-core Architectures， 2017
  • csma3: The IEEE 802.3 CSMA/CD protocol is designed for networks with a single channel and specifies the behaviour of stations with the aim of minimising simultaneous use of the channel.
  • coin6: The shared coin protocol of the randomised consensus algorithm of Aspnes and Herlihy [204]. coin-2/4/8 have the same structure but with different size of state space.
  • rabin4: The choice coordination problem (distributed consensus)

---

Markov decision process parallel value iteration algorithm on GPU §

Peng Chen et al., ISCA 2013

• progress: 60%, link
• 主要工作：实现了串行和并行的value iteration算法 举例使用的模型：基于概率状态转移的寻路问题（out of play model）

---

On the robust mapping of dynamic programming onto a graphics processing unit §

Shucai Xiao, et al., ICPDS 2009

• progress: 40%, link
• Improve the computational efficiency on the mid-level (improving memory access and synchronization efficiency)

主要工作 §

• 针对SWat(Smith-Waterman)算法提出了两种加速方案：
  • 更有效的访问GPU的global memory More efficient GPU global memory
    1. Simple implementation (matrix re-alignment)
    2. Coalesced implementation (coalesced memory access)，速度最快，将访问长度补齐
    3. Tiling wavefront，速度最慢
  • GPU (rather than CPU) synchronization 因为数据将跨block/跨multiprocessor共享，因此提出了不需要host CPU参与的GPU synchronization Share the data across block/multiprocessor, therefore design a GPU synchronization does not require CPU to involve.
    • 具体方法： 通过__threadfence()和原子操作为flag置位完成block之间的同步 参考关于CUDA中__threadfence的理解
    • 局限：为了避免互锁inter-lock问题的出现，thread block和SM必须一一对应。即启动的block数量不能超过GPU上SM的数量
• 存在的问题：
  • 最直接运用GPU的方法：简单的将算法在GPU的每个multiprocessor上复制 The most straight forward method of using GPU: duplicate the algorithm on each multiprocessor. 问题规模和提升速度受到GPU每个multiprocessor可用shared memory和cache限制。 Existing problem：Problem scale and speed-up is limited by the shared memory and cahce of each multiprocessor. What is “embarrassingly parallel ensemble”？
  • GPU的Fine-grained parallelization需要额外的multiprocessor之间的同步步骤，增加了延迟，因此一般使用coarse-grained approach Fine-grained parallelization on GPU needs extensive communication between the multiprocessors of a GPU，so usually use coarse-grained approach

Accelerating global memory access §

• 三种方法进行内存填充和运算（选择其一） Three method to filling the memory for computation (choose one from the three)
  1. Matrix re-alignment（ref to as simple implementation）
     • 行矩阵将元素移动至反对角线上 from row-major data format to a diagonal-major data format
  2. Coalesced memory access
     • padding data for coalesced memory access
  3. Tiling
     • Assigns a thread block to compute a tile. A gird of blocks is mapped to process a single tile-diagonal（tiled-wavefront）
     • 通过减少numver of kernel launches减少了同步所需的时间 Reduce the numver of kernel launches -> reduce the time costed by synchronization.

GPU synchronization §

• 存在的问题：global memory communication inter-block
• 解决方案：one-to-one mapping between the SM and the thread block

性能分析 §

• 3种Global memory access策略 x 2种同步策略（CPU/GPU），共六种方案 3 global memory access methods 2 sychronizing（CPU/GPU） methods = 6
• Execution (matrix-filling) time (比较六种策略在kernel上block数量不同时的表现) Execution (matrix-filling) time (comparing the performance of 6 methods when there are different number of blocks on a kernel)
  1. total execution (matrix filling) time coalesed < simple < tiled wavefront coalesced need fewer data transactions to fill the matrix
  2. profile of the time spent computing vs. synchronizing in the matrix-filling phase on the GPU kernel上blocks数量对性能的影响 How the number of blocks on a kernel affects the performance
  3. (Not important) Cell/BE vs. GPGPU
• Computation vs. sychronization on the GPU 同步所用时间占比由少到多： Synchronization time from low to high: Tiled < coalesced < simple

---

A scalable GPU-based approach to accelerate the multiple-choice knapsack problem §

Bharath Suri, et al., DATE 2012

• link

---

Toward efficient architecture-independent algorithms for dynamic programs §

Mohammad Mahdi Javanmard, et al., PPoPP 2019

• progress: 10%, type: full paper & poster

• 主要工作:

  • 提出了算法： A class of grid-based parallel recursive divide-&-conquer algorithms for solving dynamic programming problems can be run with provably optimal or near-optimal performance bounds on fat cores, thin cores, and purely distributed-memory machines without changing their basic strcture. 一类经过优化的，用于在CPU/GPU/分布式系统上运行的， 并行实现递归分治的算法 主要处理在使用不同并行架构加速时，如何让数据更好的适应异构内存，从而通过减少内存读写耗时提高算法效率
  • (Poster version)
    • （term）：用一类grid-based parallel recursive divide-&-conquerrecursive divide-&-conquer算法解决DP问题
    • 将2-way 扩展至r-way
    • 如何将算法扩展到external-memory GPU与distributed-memory的架构上
  • Paper version：
    • 如何将为shared-memory multicore设计的2-way recursive divide-and-conquer算法扩展至manycore GPUs和distribute-memory machines上
      • 现有方法存在的问题：计算过程中当前数值往往依赖前一次计算的数值结果，但未考虑内存异构的情况（更常访问的变量放在寄存器中）
      • 对于这个问题的一般解决方法：Tiled looping，但是必须知道smaller memory level的尺寸，对于不同架构，具体的解决代码不一样
      • 一般的r-way divide-&-conquer DP算法：解决了memory size和层次必须已知的问题，但是不适用于GPU这种对recursion支持受限，并且需要对内存进行复杂操作的架构

• References/terms to check

  • Cache-adaptive algorithms, 2014，如何在cache的层面进行优化
  • cache-adaptive, cached-oblivious, ideal cache

• 问题：

  • Shared-memory (multi- and many cores)和distributed-memory有什么区别？
    • shared-memory是在处理器内部的
    • distributed-memory是在分布式系统间的

---

Dynamic programming parallelization of matrix chain multiplication on GPU: a comparative study §

Tausif Diwan, et al., Artificial Intelligence and Evolutionary Computations in Engineering Systems, 2016

• progess: 40%

• 主要工作：

  • Thread-level多核/GPU的针对matrix chain multiplication的优化及实现

    • 在OpenMP和GPU上实现了并行的的算法，未对算法进行过多改进
    • 主要是对CPU多核（OpenMP实现）和GPU（CUDA）实现的效率比较
    • 没有随着问题的求解动态配置Threads数，而是选取了多个固定的Threads数进行对比

    traditional	GPU

    • 算法时间复杂度为，共三层循环
      1. 矩阵链的长度（子链）
      2. 子链的起始矩阵（同时由长度可知结束矩阵）
      3. 子链的拆分位置
    • GPU并行优化（所以理论上是？）：
      • CPU负责第一层循环（子链长度为2,3,…,n）
      • 第二层循环为thread并行执行
      • 将第三层循环放在thread内串行执行 一个thread的工作：给定一个子链，循环得出其在不同位置拆分的代价，找出针对这个子链的最优解，m[i, j]和s[i, j]

• 问题：

  • 有没有可能将第二层循环和第三层循环都打散到并行thread中？

---

A CUDA approach to compute perishable inventory control policies using value iteration §

G. Ortega, et al., The journal of supercomputing, 2019

• progress: 60%

• 主要工作：

  • 实际问题：perishable inventory control
  • 参考文献的层次：
    1. 用CUDA在GPU上实现VI (value iteration) process
    2. 通过OpenCL实现了用于path finding problem的VI
    3. 用HPC为traffic control table实现大尺寸的MDP
    4. 将MDP model加速用于crowd navigation (simulation)
  • 提出的方法： 将SDP(stochastic dynamic programming)/value iteration用于简化的retailer inventory control模型，模型包含了一个或者两个product，评估了对GPU的使用
  • 具体工作（解决方法存在的问题）：如何从GPU的角度实现针对perishable inventory control模型的SDP/VI
  • 如何分析computational burden:
    • Measure the number of states
    • computational time of a Matlab implementation for several instances
    • 可能GPU的实现还是用的Matlab
    • 性能提升：整体速度提升11.7x，GPU替换部分速度提升19.6x

• 实现

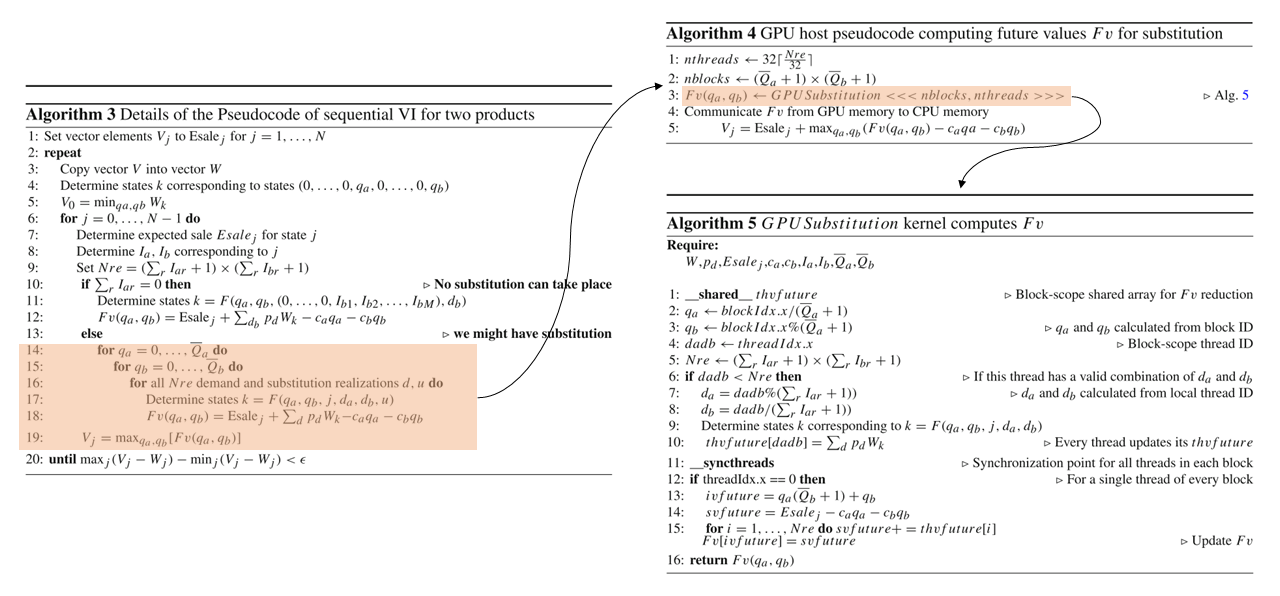
  We spawn as many blocks as combinations , i.e., up to a total of blocks, and each block contains, at least, as many threads as combinations , i.e., a total of threads.

---

GPU-Based Markov Decision Process solver §

Ársæll Þór Jóhannsson, Master thesis 2009