Plücker coordinates
- 角速度在数学意义上和向量求导的操作是可以等价的(Rigid Body Dynamics Algorithms,p23,Section 2.9)
,即速度可表示为角速度和半径向量的叉积。 此时可视作将 映射至 的操作。
- (Rigid Body Dynamics Algorithms, Section 2.9 Spatial Cross Products, p24)假设只有
轴的旋转,那么 不会产生变化, 与 应视作一般的向量。考虑 平面内的运动, 的变化(黑色->蓝色)为其叠加上一个向量(红色),这个向量的方向可以用 近似,大小(scalar)用 近似。即 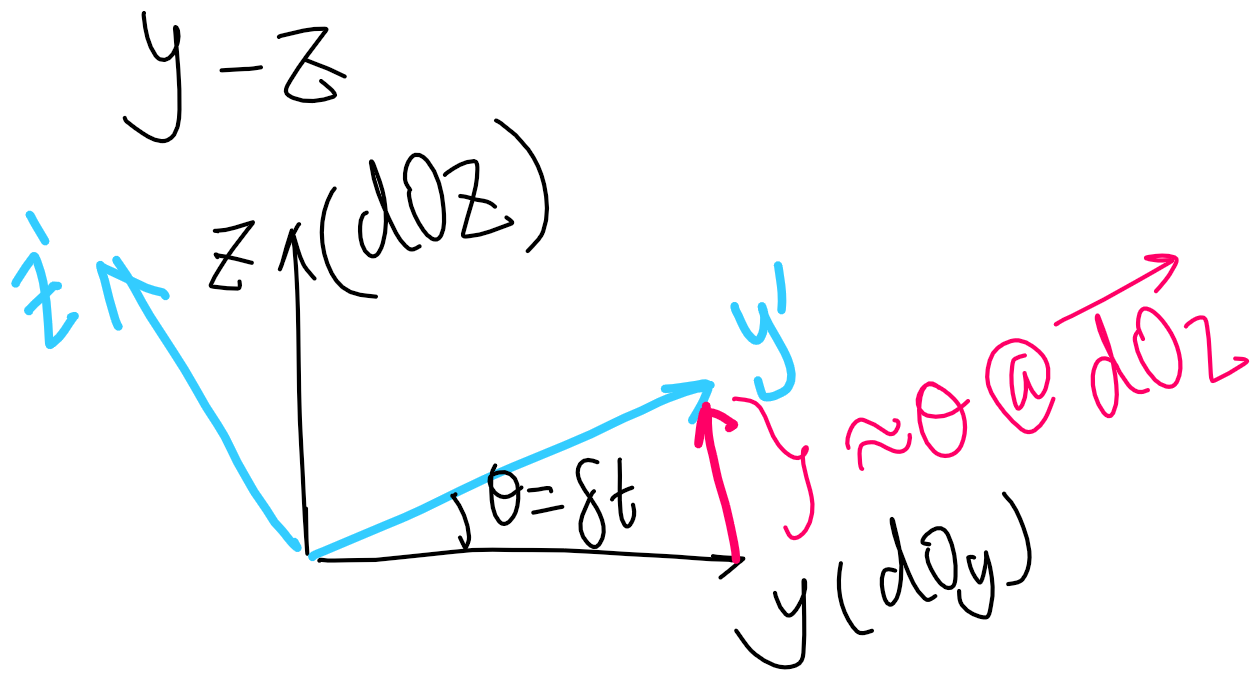
-
用上面类似的方法,可以推出在Plücker coordinates下,单位向量间完整的关系可写作:
, , 即 (Figure 2.5 (a),行叉乘列) -
得出上表后回顾前面的假设:
- 书中示例假设沿
轴旋转 ,那么旋转可表示为 。在 方向上为 由Figure 2.5(a)的表格可知 即 - 类似的,考虑
轴 得到
- 书中示例假设沿
-